POSITIVITY OF THE TRANSMUTATION OPERATORS
AND ABSOLUTE CONTINUITY OF THEIR
REPRESENTING MEASURES FOR
A ROOT SYSTEM ON Rd
AND ABSOLUTE CONTINUITY OF THEIR
REPRESENTING MEASURES FOR
A ROOT SYSTEM ON Rd
Abstract. We consider the transmutation operators 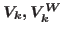 and
and
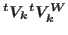 associated respectively with the Cherednik
operators and the Heckman-Opdam theory, called also in [9], [10] the
trigonometric Dunkl intertwining operators and their dual paper. In
this paper we prove that the operators
associated respectively with the Cherednik
operators and the Heckman-Opdam theory, called also in [9], [10] the
trigonometric Dunkl intertwining operators and their dual paper. In
this paper we prove that the operators 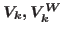 and
and
 are positivity preserving and allows positive integral
representations. Next we study the absolute continuity of their
representing measures and we deduce that the Opdam-Cherednik kernel
and the Heckman-Opdam hypergeometric function are positive definite.
are positivity preserving and allows positive integral
representations. Next we study the absolute continuity of their
representing measures and we deduce that the Opdam-Cherednik kernel
and the Heckman-Opdam hypergeometric function are positive definite.
AMS Subject classification: 33E30,33C67, 47B34, 51F15
Keywords and phrases: Cherednik operators, Heckman-Opdam theory, root system on Rd, transmutation operators, trigonometric Dunkl intertwining operators, absolute continuity of the representing measures
Download full article from here (pdf format).
DOI: 10.12732/ijam.v28i4.10
Volume: 28
Issue: 4
Year: 2015

