IJAM: Volume 28, No. 5 (2015)

Abstract. In this paper we present a family of identities for recursive sequences arising from a second order recurrence relation, that gives instances of Zeckendorf representation. We prove these results using a special case of an universal property of the recursive sequences. In particular cases we also establish a direct bijection. Besides, we prove further equalities that provide a representation of the sum of 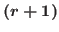-st and 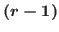-st Fibonacci number as the sum of powers of the golden ratio. Similarly, we show a class of natural numbers represented as the sum of powers of the silver ratio.