GENERALIZATION OF THE WIMAN-VALIRON
METHOD FOR FRACTIONAL DERIVATIVES
Igor Chyzhykov1, Nadiya Semochko2
1,2Faculty of Mechanics and Mathematics
Ivan Franko National University of Lviv
Universytets'ka Str. 1
Lviv, 79000, UKRAINE
Abstract. We generalize the Wiman-Valiron method for fractional derivatives proving that

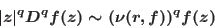
\begin{displaymath}\vert z\vert^q D^q f(z) \sim ( {\nu(r,f)})^q f(z)\end{displaymath}

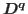holds in a neighborhood of a maximum modulus point outside an exceptional set of values of $\vert z\vert$ as $\vert z\vert\to\infty$, where $D^q$ is the Riemann-Liouville fractional derivative of order 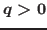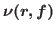$q>0$, $\nu(r,f)$ is the central index of the Taylor representation of 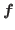$f$. We use this result to find the precise value for the order of growth of solutions of a fractional differential equation.
AMS Subject Classification: 30E15, 26A33, 34A08
Key Words and Phrases: transcendental entire function, Wiman-Valiron method, Riemann-Liouville fractional derivative, Riemann-Liouville fractional integral, fractional differential equation


Download full article from here (pdf format).

DOI: 10.12732/ijam.v29i1.3

Volume: 29
Issue: 1
Year: 2016