HAUSDORFF PROPERTY OF CARTESIAN
AND WREATH PRODUCT OF HYPERGRAPHS
AND WREATH PRODUCT OF HYPERGRAPHS
Abstract. A hypergraph
 is said to be a Hausdorff hypergraph if for any two distinct vertices
is said to be a Hausdorff hypergraph if for any two distinct vertices 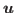 and
and 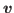 of
of 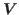 there exist hyperedges
there exist hyperedges  ,
, 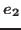
 such that
such that  ,
, 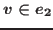 and
and
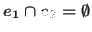 . In this paper we derive sufficient conditions for cartesian and wreath products of two hypergraphs to be Hausdorff.
. In this paper we derive sufficient conditions for cartesian and wreath products of two hypergraphs to be Hausdorff.
AMS Subject Classification: 05C65
Key Words and Phrases: Hausdorff hypergraph, Cartesian product, wreath product
Download full article from here (pdf format).
DOI: 10.12732/ijam.v29i3.10
Volume: 29
Issue: 3
Year: 2016

