ON PÓLYA AND STEFFENSEN INTEGRAL INEQUALITIES
FOR TRIGONOMETRICALLY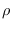 $\rho$-CONVEX FUNCTIOns
Nashat Faried1, Mohamed S.S. Ali2, Asmaa A. Badr2
1Department of Mathematics
Faculty of Science
Ain Shams University, Cairo, EGYPT
2Department of Mathematics
Faculty of Education
Ain Shams University, Cairo, EGYPT

Abstract

The aim of this article is to derive several Pólya and Steffensen type integral inequalities for trigonometrically $\rho$-convex functions.

Citation details of the article



Journal: International Journal of Applied Mathematics
Journal ISSN (Print): ISSN 1311-1728
Journal ISSN (Electronic): ISSN 1314-8060
Volume: 31
Issue: 6
Year: 2018

DOI: 10.12732/ijam.v31i6.7

Download Section



Download the full text of article from here.

You will need Adobe Acrobat reader. For more information and free download of the reader, please follow this link.

References

  1. [1] M.S.S. Ali, On certain properties of trigonometrically ρ-convex functions, J. of Advances in Pure Mathematics, 8, No 2 (2012), 337-340.
  2. [2] M.S.S. Ali, On Hadamard’s inequality for trigonometrically ρ-convex functions, RGMIA Res. Rep. Coll. (2018), Art. # 8, 7 pp.; http://rgmia.org/papers/v21/v21a08.pdf.
  3. [3] F.G. Avhadief and D.V. Maklakkov, A theory of pressure envelopes for hydrofoils, J. of Ship Technology Research, 42 (1995), 81-102.
  4. [4] E.F. Beckenbach, Convex functions, Bull. of the Amer. Math. Soc., 54, No 5 (1948), 439-460.
  5. [5] J.W. Green, Support, convergence, and differentiability properties of generalized convex functions, Proc. of the Amer. Math. Soc., 4, No 3 (1953), 391-39.
  6. [6] G. Klambauer, Problems and Propositions in Analysis, Lecture Notes in Pure and Appl. Math. 49, Marcel Dekker, New York and Basel (1979).
  7. [7] B.Ya. Levin, Lectures on Entire Functions, American Mathematical Society (1996).
  8. [8] L.S. Maergoiz, Asymptotic Characteristics of Entire Functions and Their Applications in Mathematics and Biophysics, Kluwer Acad. Publishers, New York (2003).
  9. [9] D.S. Mitrinovi´c and I.B. Lackovi´c, Hermite and convexity, Aequationes Mathematicae, 28, No 3 (1985), 229-232.
  10. [10] C.P. Niculescu and L.E. Person, Convex Functions and Their Applications A Contemporary Approach, Springer Science+Business Media, Inc. (2006).
  11. [11] G. P´olya, Ein mittelwertsatz f¨ur Funktionen mehrerer Ver¨anderlichen, Tˆohoku Math. J., 19 (1921), 1-3.
  12. [12] G. P´olya and G. Szeg¨o, Problems and Theorems in Analysis, Vol. I, Classics in Mathematics, Springer-Verlag, Berlin (1998).
  13. [13] F. Qi, P´olya type integral inequalities: Origin, variants, proofs, refinements, generalizations, equivalences, and applications, RGMIA, Res. Rep. Coll., 16 (2013), Article # 20, 32 pp.; at http://rgmia.org/v16.php.
  14. [14] A.W. Roberts and D.E. Varberg, Convex Functions, Academic Press, New York (1973).
  15. [15] J.F. Steffensen, On certain inequalities and methods of approximation, Candinavisk Aktuarietids Krift, 51, No 3 (1919), 274-297.