FUNCTIONAL ORDER DERIVATIVES
AND THE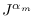 $J^{\alpha_m}$ OPERATOR
Ralph H. France III1, Sharon Careccia2
1,2 CBX 82, Dept. of Chemistry, Physics, and Astronomy
Georgia College & State University
Milledgeville, GA - 31061, USA

Abstract

The bulk of theoretical physics involves the solutions of differential equations, which are traditionally derived from a set of theoretical axioms. The authors consider the possibility that a function and its derivative are known, possibly from experimental results, while the order of the derivative is not. In most such cases there is no constant solution. The functional calculus approach to fractional derivatives is used to develop a definition of the $J^{\alpha_m}$ operator in one dimension, which differentiates a function with a different order at each point in space.

Citation details of the article



Journal: International Journal of Applied Mathematics
Journal ISSN (Print): ISSN 1311-1728
Journal ISSN (Electronic): ISSN 1314-8060
Volume: 32
Issue: 5
Year: 2019

DOI: 10.12732/ijam.v32i5.9

Download Section



Download the full text of article from here.

You will need Adobe Acrobat reader. For more information and free download of the reader, please follow this link.

References

  1. [1] S. Kempfle, I. Schafer, H Beyer, Functional calculus and a link to fractional calculus, Fract. Calc. Appl. Anal. 5, No 4 (2002), 411-426.
  2. [2] R. Shankar, Principles of Quantum Mechanics. 2n Ed., Springer Science, New York (2008).