A NEW IMPROVED RUNGE-KUTTA FORMULA
FOR DIRECTLY SOLVING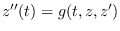 $z''(t)=g(t,z,z')$
Kasim Abbas Hussain1, Fudziah Ismail2
1Department of Mathematics, College of Science
Mustansiriyah University, Baghdad, IRAQ
2 Department of Mathematics
and Institute for Mathematical Research
Universiti Putra Malaysia
43400 UPM Serdang, Selangor, MALAYSIA

Abstract

This paper deals with the derivation of an explicit two-stage third-order Improved Runge-Kutta Nyström (IRKNG) method for directly solving general second order ordinary differential equations (ODE). This method is two-step and the number of functions to be evaluated per step is less via comparsion to the existing RK methods. Numerical outcomes are offered to show the validity and competency of the newly IRKNG method as comparison with the general RKN and RK techniques.

Citation details of the article



Journal: International Journal of Applied Mathematics
Journal ISSN (Print): ISSN 1311-1728
Journal ISSN (Electronic): ISSN 1314-8060
Volume: 33
Issue: 1
Year: 2020

DOI: 10.12732/ijam.v33i1.3

Download Section



Download the full text of article from here.

You will need Adobe Acrobat reader. For more information and free download of the reader, please follow this link.

References

  1. [1] E. Hairer, S.P. Nørsett, G. Wanner, Solving Ordinary Differential Equations I: Nonstiff Problems, Springer, Berlin (1993).
  2. [2] P.R. Holland, The Quantum Theory of Motion, Cambridge University Press, Cambridge (2000).
  3. [3] V.A. Avdyushev, Special perturbation theory methods in celestial mechanics, I. Principles for the construction and substantiation of the application, Russian Phys. J., 49 (2006), 1344-1253.
  4. [4] J.C. Butcher, Numerical Methods for Ordinary Differential Equations, 2nd ed., Wiley, New York (2008).
  5. [5] E. Hairer, G. Wanner, A theory for Nyström methods, Numer. Math. 25 (1976), 383-400.
  6. [6] M.M. Chawla, S.R. Sharma, Families of three-stage third order Runge Kutta Nyström methods for y′′ = f (x, y, y ′ ), J. Aust. Math. Soc., 26 (1985), 375-386.
  7. [7] B.P. Sommeijer, Explicit, high-order Runge Kutta Nyström methods for parallel computers, Appl. Numer. Math., 13 (1993), 221-240.
  8. [8] E. Hairer, Méthodes de Nyström pour l’équation différentielle y ′′ = f (x, y), Numer. Math., 27 (1976), 283-300.
  9. [9] J.M. Franco, Exponentially fitted symplectic integrators of RKN type for solving oscillatory problems, Comput. Phys. Comm., 177 (2007), 479-492.
  10. [10] H. Yang, X. Wu, X. You, Y. Fang, Extended RKN-type methods for numerical integration of perturbed oscillators, Comput. Phys. Comm., 180 (2009), 1777-1794.
  11. [11] X. You, J. Zhao, H. Yang, Y. Fang, X. Wu, Order conditions for RKN methods solving general second-order oscillatory systems, Numer. Algor., 66 (2014), 147-176.
  12. [12] D.O. Awoyemi, A new sixth-order algorithm for general second order ordinary differential equation, International Journal of Computer Mathematics, 77 (2001), 117-124.
  13. [13] F. Rabiei, F. Ismail, N. Senu, N. Abasi, Construction of Improved RungeKutta Nyström method for solving second-order ordinary differential equations, World Applied Sciences Journal, 20 (2012), 1685-1695.
  14. [14] F. Rabiei, F. Ismail, Third-order Improved Runge-Kutta method for solving ordinary differential equation, International Journal of Applied Physics and Mathematics, 1 (2011), 191-194.
  15. [15] O. Abu Arqub, A. El-Ajou, A.S. Bataineh, I. Hashim, A Representation of the exact solution of generalized Lane-Emden equations using a new analytical method, Abstract and Applied Analysis, 2013 (2013), 1-10.
  16. [16] J. Vigo-Aguiara, H. Ramos, Variable stepsize implementation of multistep methods for y ′′ = f (x, y, y ′), Journal of Computational and Applied Mathematics, 192 (2006), 114-131.