DIAGONAL MATRIX SCALING
AND H-MATRICES
AND H-MATRICES
Abstract. The iterative methods for characterization of H-matrices consider the problem of finding a
positive diagonal matrix 
such that 
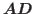is strictly diagonally dominant.
In this paper we consider this property and use the Gordan's theorem of the alternative
to find a linear feasibility problem which can be solved efficiently by
pivoting methods and gives us a criterion for deciding about the H-character of a given matrix.
We also describe matrix scaling problem and show that there is a matrix corresponding
to any given matrix 
such that its scalability is equivalent to the H-character of .
such that is strictly diagonally dominant.
In this paper we consider this property and use the Gordan's theorem of the alternative
to find a linear feasibility problem which can be solved efficiently by
pivoting methods and gives us a criterion for deciding about the H-character of a given matrix.
We also describe matrix scaling problem and show that there is a matrix corresponding
to any given matrix such that its scalability is equivalent to the H-character of .
AMS Subject Classification: 15B99, 65F10
Keywords and phrases: H-matrix, generalized strictly diagonally dominant, linear feasibility problem, diagonal matrix scaling
Download full article from here (pdf format).
DOI: 10.12732/ijam.v28i5.1
Volume: 28
Issue: 5
Year: 2015
