BLOW-UP FOR DISCRETIZATIONS OF SOME
REACTION-DIFFUSION EQUATIONS WITH
A NONLINEAR CONVECTION TERM
Diabate Nabongo1, N'Guessan Koffi2, Toure Kidjegbo Augustin3
1,2Alassane Ouattara University of Bouake
UFR SED
Bouake, P.O. Box V18 Bouake, IVORY COST
3National Polytechnic Institute Houphouet Boigny
Department of Mathematics
Yamoussoukro, P.O. Box 1093 Yamoussoukro, IVORY COST

Abstract

This paper concerns the study of the numerical approximation for the following parabolic equations with a nonlinear convection term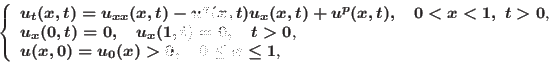

\begin{displaymath}% \\ \left\{ % \begin{array}{ll} \hbox{$u_t(x,t)=u_{xx}(x... ..._{0}(x) > 0,\quad 0\leq x \leq 1$,} \\ \end{array}% \right. \end{displaymath}

where $q\geq 1$ and $p\geq q+1$.

We find some conditions under which the solution of the discrete form of the above problem blows up in a finite time and estimate its numerical blow-up time. We also prove that the numerical blow-up time converges to the real one, when the mesh size goes to zero. Finally, we give some numerical experiments to illustrate ours analysis.

Citation details of the article



Journal: International Journal of Applied Mathematics
Journal ISSN (Print): ISSN 1311-1728
Journal ISSN (Electronic): ISSN 1314-8060
Volume: 29
Issue: 5
Year: 2016

DOI: 10.12732/ijam.v29i5.4

Download Section



Download the full text of article from here.

You will need Adobe Acrobat reader. For more information and free download of the reader, please follow this link.

References

  1. [1] L.M. Abia, J.C. Lopez-Marcos and J. Martinez, On the blow-up time convergence of semidiscretizations of reaction-diffusion equations, Appl. Numer. Math., 26 (1998), 399-414.
  2. [2] J. Bec, K. Khanin, Burgers turbulence, Physics Reports, 447 (2007), 1-66.
  3. [3] J. von Below, An existence result for semilinear parabolic network equations with dynamical node conditions, In: Progress in Partial Differential Equations: Elliptic and Parabolic Problems, Pitman Research Notes Math. Ser. Longman Harlow Essex, # 266 (1992), 274-283.
  4. [4] J. von Below, Parabolic Network Equations, Tubingen, 2 Ed. (1994).
  5. [5] J. von Below, C. De Coster, A qualitative theory for parabolic problems under dynamical boundary conditions, J. of Inequalities and Applications, 5 (2000), 467-486.
  6. [6] J. von Below, S. Nicaise, Dynamical interface transition in ramified media with diffusion, Comm. Partial Differential Equations, 21 (1996), 255-279.
  7. [7] J. von Below, G. Pincet-Mailly, Blow up for reaction diffusion equations under dynamical boundary conditions, Communications in Partial Differential Equations, 28 (2003), 223-247.
  8. [8] J. von Below, G. Pincet-Mailly, Blow-up for some nonlinear parabolic problems with convection under dynamical boundary conditions, Discrete and Continuous Dynamical Systems, Supplement Vol. (2007), 1031-1041.
  9. [9] J. von Below, G. Pincet-Mailly, J-F. Rault, Growth order and blow-up points for the parabolic Burgers’ equation under dynamical boundary conditions, Discrete Contin. Dyn. Syst. Ser. S., 6, No 3 (2013), 825-836.
  10. [10] T.K. Boni, H. Nachid and D. Nabongo, Blow-up for discretization of a localized semilinear heat equation, Annals of the Alexandru Ioan Cuza University-Mathematics, 56, No 1 (2010), 385-406.
  11. [11] S. Chen, Global existence and blow-up of solutions for a parabolic equation with a gradient term, Proc. Amer. Math. Soc., 129 (2001), 975-981.
  12. [12] M. Chipot, F.B. Weissler, Some blow-up results for a nonlinear parabolic equation with a gradient term, SIAM J. Math. Anal., 20 (1989), 886-907.
  13. [13] M. Chlebik, M. Fila, P. Quittner, Blow-up of positive solutions of a semilinear parabolic equation with a gradient term, Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal., 10 (2003), 525-537.
  14. [14] A. Constantin, J. Escher, Global existence for fully parabolic boundary value problems, NoDEA , 13 (2006), 91-118.
  15. [15] J. Ding, Blow-up solutions for a class of nonlinear parabolic equations with Dirichlet boundary conditions, Nonlinear Anal., 52 (2003), 1645-1654.
  16. [16] J. Ding, B.-Z. Guo, Global and blow-up solutions for nonlinear Parabolic equations with a gradient term, Houston Journal of Mathematics, 37, No 4 (2011), 1265-1277.
  17. [17] J. Ding, B.-Z. Guo, Global existence and blow-up solutions for quasilinear reaction-diffusion equations with a gradient term, Applied Mathematics Letters, 24 (2011), 936-942.
  18. [18] M. Fila, Remarks on blow-up for a nonlinear parabolic equation with a gradient term, Proc. Amer. Math. Soc., 111 (1991), 795-801.
  19. [19] U. Frisch, Turbulence: The Legacy of A.N. Kolmogorov, Cambridge University Press (1995).
  20. [20] G.R. Goldstein, Derivation and physical interpretation of general boundary conditions, Adv. in Diff. Equ., 11 (2006), 457-480.
  21. [21] O. Ladyzenskaya, V. Solonnikov, N. Uraltseva, Linear and Quasilinear Equations of Parabolic Type, Transl. of Math. Monographs, # 23 (1968).
  22. [22] P.E. Mensah, M.M. Taha, A.K. Toure, Numerical approximation of the blow-up time for a semilinear parabolic equation with nonlinear boundary conditions, Far East J. of Math. Sciences (FJMS), 60, No 45 (2012), 125-167.
  23. [23] K. N’Guessan, D. Nabongo and A.K. Toure, Blow-up for semidiscretizations of some semilinear parabolic equations with a convection term, J. of Progressive Research in Mathematics (JPRM), 5, No 2 (2015), 499-518.
  24. [24] G. Pincet-Mailly, J-F. Rault, Nonlinear convection in reaction-diffusion equations under dynamical boundary conditions, Electronic J. of Differential Equations, 2013, No 10 (2013), 1-14.
  25. [25] J.-F. Rault, Phenomene d’explosion et existence globale pour quelques problmes paraboliques sous les conditions au bord dynamiques, PhD Thesis, Universite du Littoral Cˇ ote d’Opale (2010).
  26. [26] J.-F. Rault, A bifurcation for a generalized Burgers’ equation in dimension one, Discrete Contin. Dyn. Syst. Ser. S., 5, No 3 (2012), 683-706.
  27. [27] P. Souplet, Finite time blow-up for a non-linear parabolic equation with a gradient term and applications, Math. Methods Appl. Sci., 19 (1996), 1317-1333.
  28. [28] P. Souplet, Recent results and open problems on parabolic equations with gradient nonlinearities, Electronic J. of Differential Equations, 2001, No 20 (2001), 1-19.
  29. [29] P. Souplet, F. Weissler, Self-similar subsolutions and blow-up for nonlinear parabolic equations, J. of Mathematical Analysis and Applications, 212 (1997), 60-74.
  30. [30] P. Souplet, S. Tayachi, F.B. Weissler, Exact self-similar blow-up of solutions of a semilinear parabolic equation with a nonlinear gradient term, Indiana Univ. Math. J., 45 (1996), 655-682.
  31. [31] A.K. Toure, K. N’Guessan and D. Nabongo, Blow-up for Semidiscretizations of some reaction-diffusion equations with a nonlinear convection term, Global J. of Pure and Applied Mathematics (GJPAM), 11, No 6 (2015), 4273-4296.
  32. [32] F. Weissler, Existence and nonexistence of global solutions for a semilinear heat equation, Israel J. of Mathematics, 38 (1981), 29-40.